Im Markt für Hebelprodukte kommt jeder Anleger unweigerlich mit Begriffen wie Hebel, Volatilität oder auch mit den sogenannten „Griechen“ wie Delta, Theta und Vega in Berührung. Was bedeuten die Kennzahlen, und wie werden sie berechnet?
Goldman Sachs verwendet für die Berechnung der Kennzahlen auf www.gs.de ein vereinfachtes Black-Scholes-Modell. Delta, Theta und die anderen griechischen Kennzahlen resultieren aus diesem Modell, das zur Preisbestimmung von Optionen häufig eingesetzt wird. Es wurde von Fischer Black, Myron Scholes und Robert Merton entwickelt. Die Optionspreisformel kann nach verschiedenen Parametern partiell abgeleitet werden. Das Ergebnis hieraus sind „die Griechen“.

Das Black-Scholes-Modell beruht auf folgenden Annahmen:
1. Die Aktien zahlen keine Dividende während der Laufzeit.
2. Die Ausübung erfolgt europäisch. Das bedeutet: Die Ausübung kann nur am Verfalltag erfolgen, bei amerikanischen Optionen ist dagegen die Ausübung an jedem Tag bis zum Verfall möglich.
3. Die Märkte sind effizient. Diese Voraussetzung bedeutet einerseits, dass kein Marktteilnehmer in der Lage ist, die Richtung der nächsten Kursbewegung zuverlässig vorauszusagen, andererseits, dass die Kurse sich kontinuierlich, also ohne Sprünge, verändern.
4. Es fallen keine Transaktionskosten an, und Marktteilnehmer können Aktien leerverkaufen.
5. Zinssätze bleiben konstant und sind allen Marktteilnehmern bekannt. Auf www.gs.de gehen wir von einem konstanten Zins von null Prozent aus.
6. Die zukünftigen Aktienkursrenditen sind lognormal um den Forward verteilt. Bei der Lognormalverteilung, also der logarithmischen Normalverteilung, handelt es sich um eine stetige Verteilung, die nur positive Werte annehmen kann.
Die griechischen Kennzahlen
Eine der wichtigsten Kennzahlen aus dem Black-Scholes-Modell ist das Delta. Es gibt an, um wie viel sich der Preis der Option ändert, wenn sich der Kurs des Basiswerts um eine Einheit ändert und alle übrigen Einflussfaktoren konstant bleiben. Das Delta kann als absolute Zahl oder als Prozentzahl angegeben werden. Es liegt bei Call-Optionsscheinen zwischen 0 und +1 bzw. zwischen 0 Prozent und +100 Prozent, bei Put-Optionsscheinen zwischen 0 und –1 bzw. zwischen 0 Prozent und –100 Prozent.
Abb. 1: Beispiel – das Delta
Der Chart 1a zeigt den inneren Wert eines Call-Optionsscheins und seinen theoretischen Wert als Funktion des Basiswertpreises im Bereich von 50 bis 150 Euro an. Im Bereich von 50 bis 70 Euro ist der Anstieg der Kurve nur gering, sie steigt, je weiter der Optionsschein ins Geld wandert, immer steiler an. Die Kennzahl, die diesen Zusammenhang beschreibt, heißt Delta. Das Delta gibt an, um wie viel sich der Preis der Option ändert, wenn sich der Kurs des Basiswerts um eine Einheit ändert und alle übrigen Einflussfaktoren konstant bleiben.
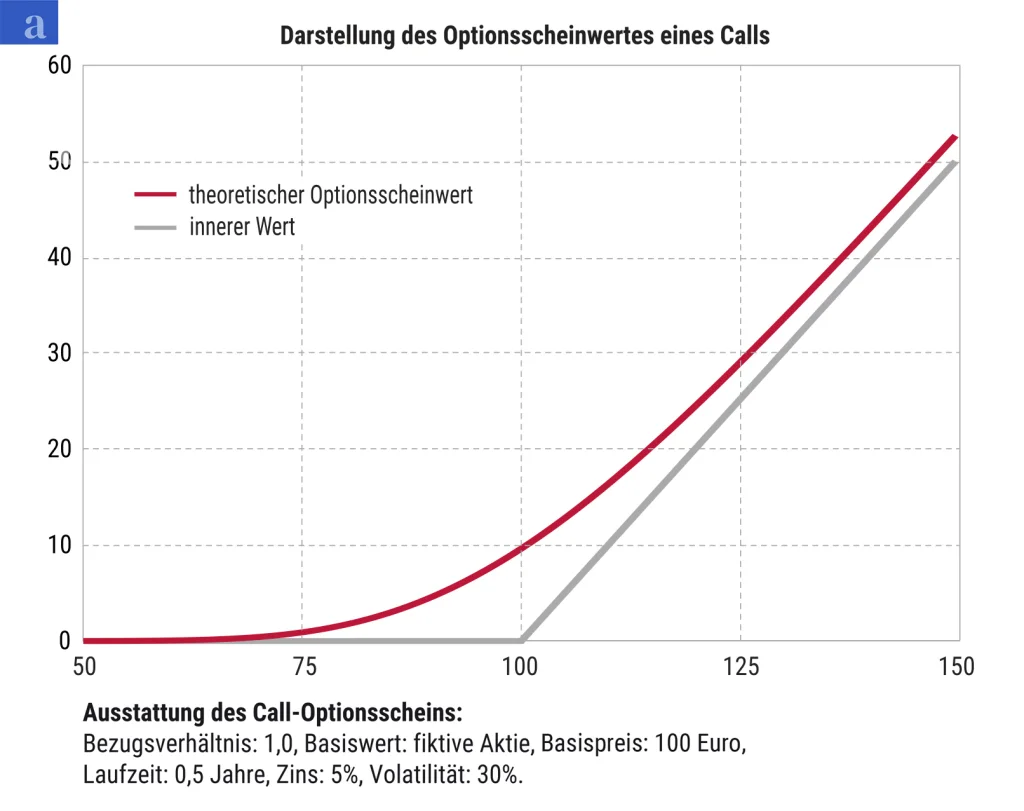
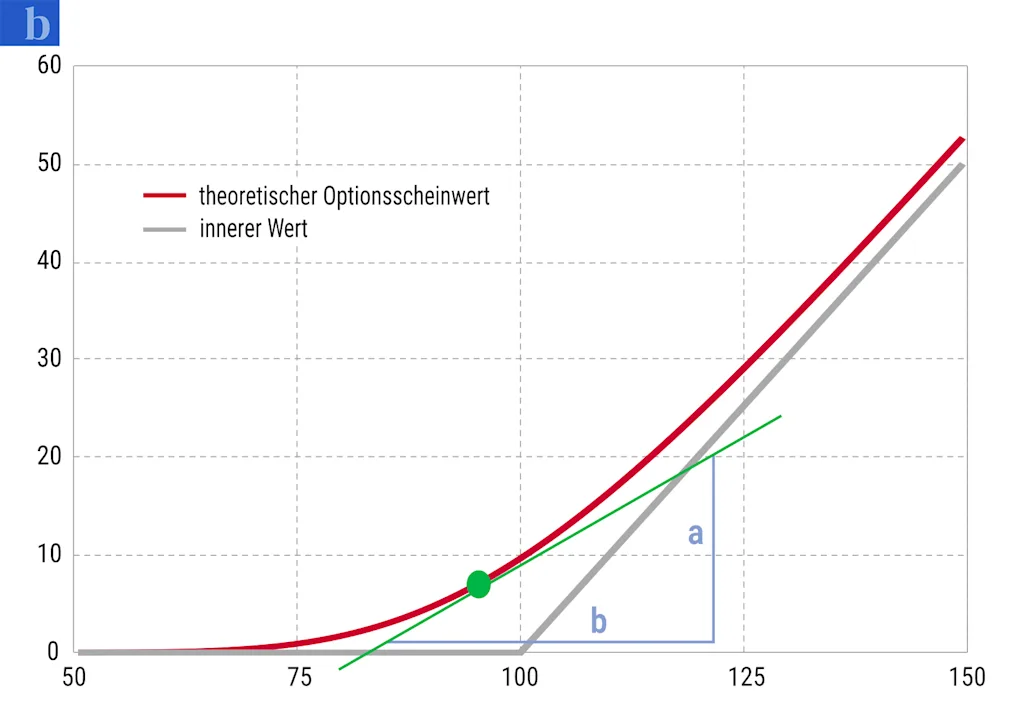
Um das Delta an einer Stelle genau zu bestimmen, wird ein Steigungsdreieck eingezeichnet und eine Tangente angelegt, die die Kurve nur in einem Punkt berührt. Die Tangente im Chart 1b berührt die Kurve in Höhe des angenommenen Kurses des Basiswerts von 95 Euro. Das Verhältnis von a zu b gibt das Delta an diesem Punkt an. In unserem Beispiel beträgt das Ergebnis 0,49. Verschiebt man den grünen Punkt gedanklich entlang der roten Kurve, zeigt sich, dass das Delta bei einem Optionsschein, der weit aus dem Geld notiert, sehr niedrig ist und ansteigt, je weiter der Optionsschein ins Geld wandert. Bei weit im Geld stehenden Optionsscheinen erreicht die Steigung genau 45 Grad, das entspricht einem Euro Wertzuwachs bei einem Anstieg des Basiswerts um einen Euro. Das Verhältnis, das die Steigung annimmt, ist dann mit 1,0 der höchste Wert, den das Delta eines Optionsscheins erreichen kann.
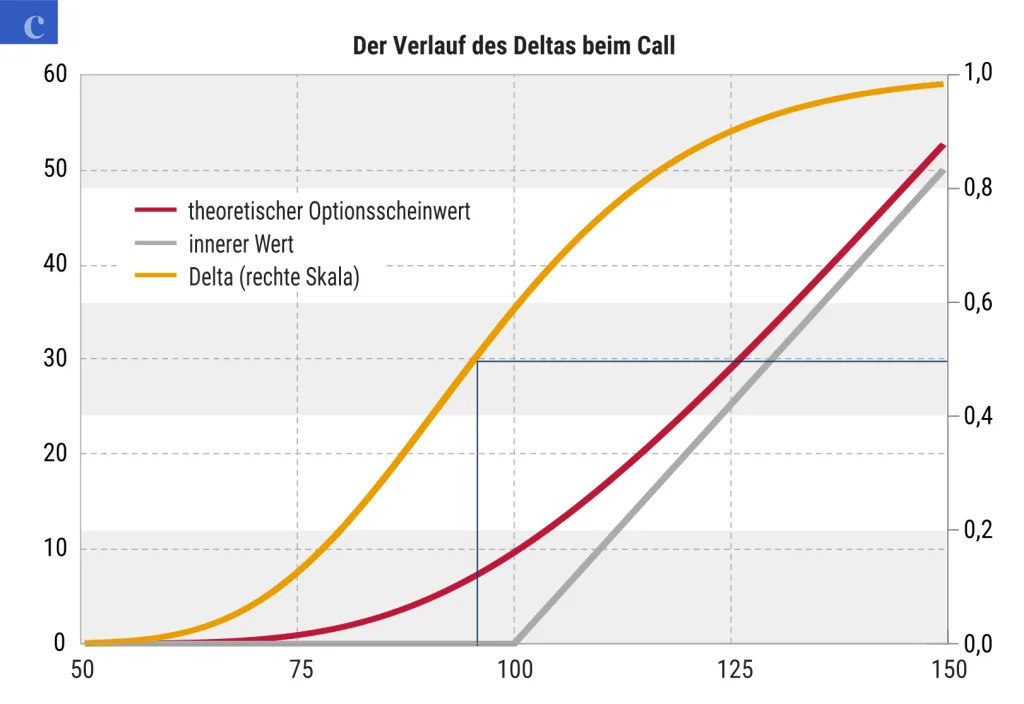
Das Delta ist in der Black-Scholes-Formel (siehe unten: Exkurs) die erste partielle Ableitung nach dem Basiswertkurs. Die gelbe Kurve im Chart 1c zeigt den Verlauf des Deltas an. In den Bereichen weit aus dem Geld und weit im Geld verläuft die Deltakurve flach. Das Delta liegt für Call-Optionsscheine zwischen 0 und +1, für Put-Optionsscheine liegt es zwischen 0 und –1. Der Chart 1c zeigt an der rechten y-Achse die Deltawerte für einen Call-Optionsschein.
Quelle: Goldman Sachs Global Markets
Das Gamma beschreibt die Änderung des Deltas. Mathematisch ausgedrückt ist das Gamma die zweite Ableitung des Optionspreises nach dem Basiswertkurs (das Delta ist die erste Ableitung). Das Gamma beschreibt die Änderung des Deltas bei einer Änderung des Basiswerts um eine Einheit. Es ist vor allem für Händler beim Hedging von Bedeutung. Aber auch Anleger können so erkennen, welcher Optionsschein ein sich besonders stark änderndes Delta aufweisen wird.
Das Vega sagt aus, um wie viel sich der Preis des Optionsscheins ändert, wenn sich die Volatilität des Basiswerts um 1 Prozentpunkt ändert. „Vega“ ist nicht wirklich ein griechischer Buchstabe, dennoch wird dieser Kunstname zu „den Griechen“ gezählt.
Das Theta gibt Aufschluss über die Intensität des Zeitwertverlusts innerhalb einer Einheit, z.B. pro Tag oder pro Woche. Auf der Website ist das Theta pro Tag angegeben.
Ein vergleichsweise wenig bekannter „Grieche“ ist das Rho. Es misst den Einfluss einer Änderung des risikolosen Zinssatzes auf den Optionsscheinpreis. Die Wirkung von Zinsveränderungen auf den Optionspreis ist meist jedoch relativ gering. Der absolute Betrag des Rho wird für einen Call mit steigenden Basiswertpreisen immer größer. Auf www.gs.de gehen wir – auch bei Währungsoptionsscheinen – von einem Zins von null Prozent aus.
Ein griechischer Buchstabe, aber kein „Grieche“ im Sinne der Black-Scholes-Formel, ist das Omega. Es errechnet sich durch Multiplikation des Deltas mit dem Hebel. Dabei wird der Hebel durch Multiplikation des Basiswerts mit dem Bezugsverhältnis geteilt durch den Briefkurs des Optionsscheins berechnet (bei Produkten in Fremdwährung bereinigt um den Wechselkurs). Im Vergleich zum Hebel gibt das Omega aber besseren Aufschluss über die Hebelwirkung eines Optionsscheins. Auf www.gs.de finden Anleger Delta, Omega, Theta und Vega.
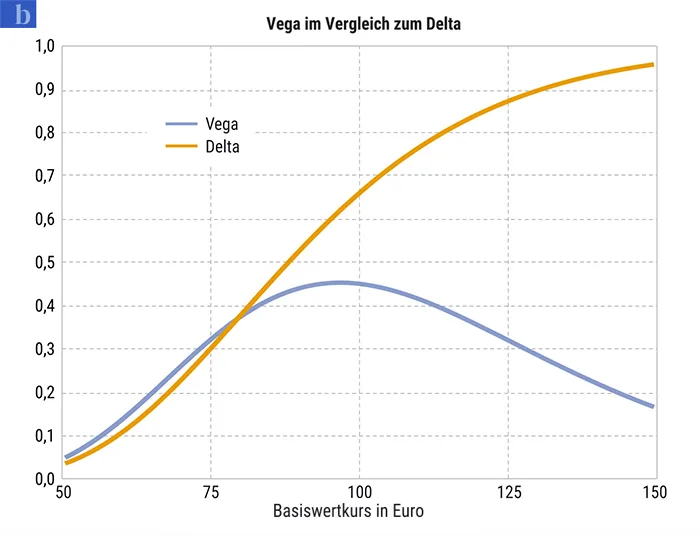
Abb. 2: Beispiel – das Vega
In dem Beispiel von Chart 2a wird ein Optionsschein mit einem Basispreis von 100 Euro angenommen, der Kurs des fiktiven Basiswerts liegt bei 90 Euro, der Zins bei 5 Prozent, die implizite Volatilität bei 30 Prozent. Daraus ergibt sich ein Optionsscheinpreis von 4,71 Euro. Wenn nun die implizite Volatilität auf 31 Prozent steigt, würde sich der Preis des Optionsscheins bei sonst unveränderten Einflussfaktoren auf 4,71 plus 0,24 Euro, also auf 4,95 Euro, erhöhen. Bei einem Absinken der impliziten Volatilität auf 29 Prozent würde der Optionsscheinpreis um 4,71 minus 0,24 Euro, also auf 4,47 Euro, sinken. Bei steigender impliziter Volatilität steigt der Wert des Optionsscheins je nach Restlaufzeit umso steiler an, je weiter der Basiswert in Richtung Geld wandert. Die Kurve wird wieder flacher, wenn der Optionsschein weit im Geld liegt.
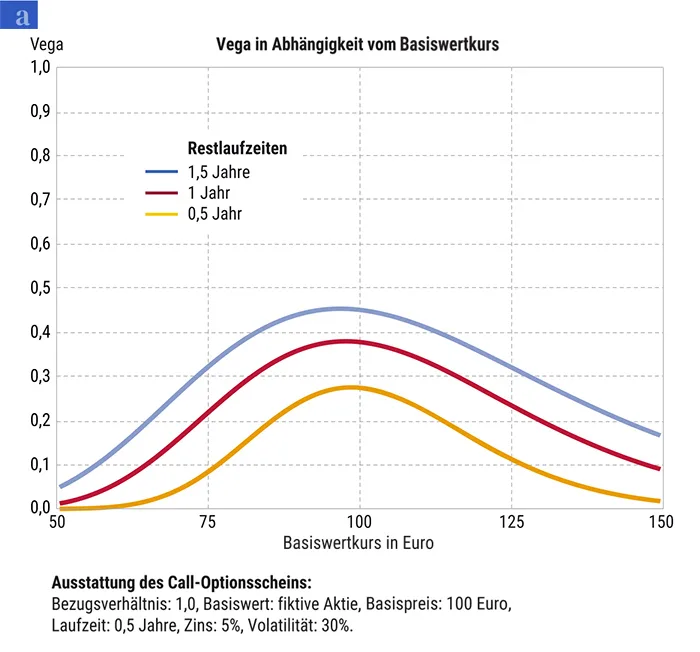
Wählt ein Anleger bei hoher Volatilität einen sehr weit aus dem Geld notierenden Call-Optionsschein aus, so profitiert er bei einem steigenden Basiswertkurs zwar vom „Deltaeffekt“. Auf der anderen Seite kann ihm eine dann sinkende Volatilität den Wertzuwachs des Optionsscheins verderben. Ein Investment in weit aus dem Geld notierende Optionsscheine erweist sich damit quasi als eine Spekulation auf die Volatilität. Sinkt die Volatilität um einen Prozentpunkt, so kann der „Vegaeffekt“ einen weitaus stärkeren Einfluss auf die Wertentwicklung eines Optionsscheins haben, als ihn ein Anstieg des Basiswerts um einen Euro hätte. Dies ist ein häufig zu beobachtender Grund dafür, dass zwar der Basiswert an Wert gewinnt, der Optionsschein jedoch nicht im Preis zulegt.
Quelle: Goldman Sachs Global Markets
Implizite Volatilität
Die Kennzahl Volatilität bezeichnet das Ausmaß der Schwankungen von Kursen an Finanzmärkten. Diese Schwankungen haben oftmals einen entscheidenden Einfluss auf die Preisentwicklung einer Vielzahl von Zertifikaten und aller Optionsscheine. Die implizite Volatilität ist die vom Markt für einen bestimmten Zeitraum erwartete Schwankungsbreite, welche sich beispielsweise aus dem Preis von an Terminbörsen, wie z.B. der Eurex, gehandelten Optionen berechnen lässt.
Dies ist möglich, da die Volatilität eine Variable in der zur Optionspreisberechnung verwendeten Black-Scholes-Formel ist und alle anderen Variablen, einschließlich des letzten gehandelten Preises einer Option, bekannt sind. Da es aber nicht möglich ist, die Black-Scholes-Formel nach der Volatilität aufzulösen und explizit auszudrücken, muss hier die Lösung durch Probieren gefunden werden. Dabei setzt man alle bekannten Variablen sowie einen Schätzwert für die Volatilität in das Optionspreismodell ein und rechnet den Wert des Optionsscheins aus. Sollte dieser Wert dann gleich mit dem Kurs des Optionsscheins übereinstimmen, hat man die richtige implizite Volatilität bereits gefunden. Häufiger jedoch werden die Zahlenwerte abweichen, und man muss weitere Iterationen durchführen, um sich schrittweise dem richtigen Ergebnis anzunähern.

Iteration beginnend mit historischer Volatilität
Das Newton-Raphson-Verfahren, das nach den beiden englischen Mathematikern Isaac Newton und Joseph Raphson benannt wurde, dient hierbei dazu, einen möglichst guten Vorschlag für den jeweils nächsten Versuch zu machen und so die Zahl der benötigten Iterationsschritte zu begrenzen. Auch die in den „Produkteigenschaften“ auf der Webseite dargestellte implizite Volatilität wird nach diesem Iterationsverfahren berechnet: Die implizite Volatilität ist die einzige Variable in der Black-Scholes-Formel, die man nicht als solche beobachten kann. Die anderen Inputs in die Formel, wie Aktienkurs, Basispreis, Zinskurs und Restlaufzeit, lassen sich gut beobachten.
Das Iterationsverfahren funktioniert im Einzelnen so: Ein zufälliger Wert für die implizite Volatilität wird in die Black-Scholes-Formel eingesetzt. Um bereits mit einem geeigneten Startwert zu beginnen, verwenden wir hierfür die historische Volatilität des Basiswerts. Das Ergebnis, also der mit der Black-Scholes-Formel berechnete Wert für die Option, wird nun mit dem tatsächlich beobachteten Wert verglichen.
Sollte das Ergebnis zu groß sein, so wird das gleiche Verfahren nun mit einer kleineren gedachten impliziten Volatilität wiederholt. Optionsscheine gewinnen an Wert, wenn die implizite Volatilität steigt. Sollte der Optionswert zu klein sein, wird das Verfahren mit einer größeren Volatilität wiederholt. Das Newton-Raphson-Verfahren liefert dann bereits einen guten Wert dafür, um wie viel die Volatilität für den nächsten Schritt erhöht oder gesenkt werden sollte, und zwar, indem auch die erste Ableitung der Optionspreisformel nach der Volatilität für den Schätzwert berechnet wird.
Mittels des Vegas wird bestimmt, um wie viel die „Vola“ höher sein müsste, um genau den Volatilitätswert zu treffen (unter der offensichtlich nicht ganz richtigen Annahme, dass das Vega für unterschiedliche Volatilitätsniveaus konstant wäre). Dementsprechend erzielt man im zweiten Schritt ein Ergebnis, das schon sehr viel besser, aber noch nicht perfekt ist.
Grenzen des Iterationsverfahrens
Wiederholt man den Vorgang aber nur wenige Male, kann man den tatsächlichen Wert immer genauer bestimmen. Dabei gilt es allerdings zu beachten, dass dieses Verfahren bei Optionsscheinen, die besonders tief im Geld oder besonders tief aus dem Geld notieren, nicht gut funktioniert, da solche Optionsscheine relativ unsensibel auf Volatilitätsänderungen reagieren. Wenn ein Optionsschein beispielsweise tief aus dem Geld notiert und daher einen geringen Briefkurs aufweist, wird das Verfahren leider unzuverlässig.
Eine weitere Einschränkung muss beim Zahlenwert für die implizite Volatilität gemacht werden: Das Black-Scholes-Verfahren bezieht sich nur auf europäische Optionen, während fast alle Optionsscheine das etwas wertvollere amerikanische Ausübungsrecht verbriefen. Daher setzen wir beim Berechnen der Preise der Optionsscheine ein aufwendigeres Modell ein als das simple Black-Scholes-Modell, sodass schon deshalb nicht der gleiche Wert in der Rückrechnung erzielt werden kann, den der Emittent zuvor bei der Berechnung der Optionsscheinpreise genutzt hat. Für einen relativen Vergleich von Optionsscheinen untereinander ist das Verfahren aber dennoch – von extremen Ausnahmen abgesehen – sehr gut geeignet.
Quelle: Goldman Sachs Global Markets
Bitte beachten Sie unsere Hinweise zu Risiken, Disclaimer und Impressum, welche hier eingesehen werden können.
Fotonachweise: Adobe Stock – Bild 1: Jeff Baumgart, Bild 2: bht2000
